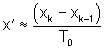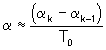DIPLOMARBEIT
INVERSES PENDEL
Fertigstellung eines Versuchsaufbaues und
Programmierung einer Echtzeit-Regelung
Verfasser:
Tobias Migge
Matrikel-Nr.: 9620
Betreuer:
Dipl. Ing. Poock-Haffmans
Vorwort
Die vorliegende Arbeit wurde im Labor für Prozeßprogrammierung der Fachhochschule Wedel von November 1995 bis Juli 1996 ausgeführt.
Ich danke Herrn Dipl.-Ing. P. Poock-Haffmans, daß er mir das Thema dieser Arbeit zur Bearbeitung überließ, und für die Unterstützung, die er mir dabei zukommen ließ.
Die Mitarbeiter des Fachbereiches Technische Informatik standen stets für zahlreiche Diskussionen zur Verfügung. Herr Dipl.-Ing. J. Völker vom Institut für anwendungsnahe Technologieanwendungen
(ITW) unterstützte mich bei der Entwicklung einer störungsunempfindlichen Meßelektrik. Herr P. Eggerstedt fertigte die Spannvorrichtung und den Pendelwagen und war maßgeblich an der Konstruktion
beider Apparaturen beteiligt. Ihnen möchte ich an dieser Stelle meinen herzlichen Dank aussprechen.
Schließlich danke ich Dr. Kahlert und seinen Mitarbeitern für die schnelle Umsetzung meiner Vorschläge bezüglich der Software WinFACT.
Hamburg, im Juli 1996
Tobias Migge
Inhaltsverzeichnis
- 1 ZUSAMMENFASSUNG
- 2 AUFGABENSTELLUNG
- 3 FERTIGSTELLUNG VERSUCHSAUFBAU
- 4 MODIFIKATION DES VERSUCHSAUFBAUES
- 5 SYSTEMANALYSE UND REGLERENTWURF
- 6 SOFTWARE
- 7 ERGEBNISSE
- 8 SCHLUSSFOLGERUNGEN UND AUSBLICK
- 9 LITERATURVERZEICHNIS
Technische Daten Versuchsaufbau
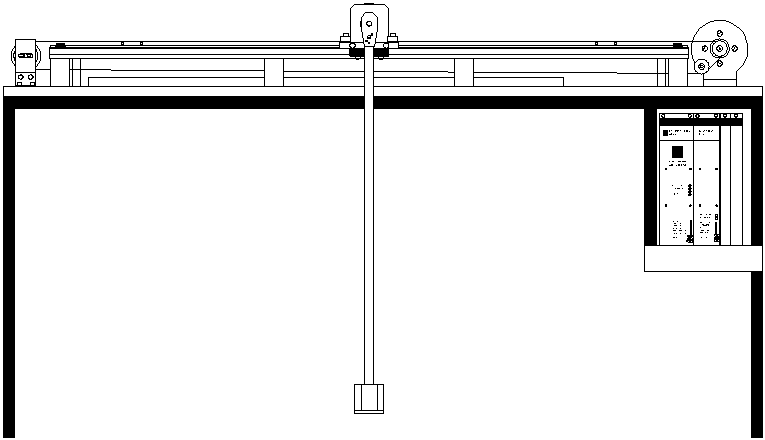
Bilder vom Versuchsaufbau
1 Zusammenfassung
In vielen Labors für Regelungstechnik finden sich Pendelsysteme, da diese einfache und anschauliche Beispiele für instabile und nichtlineare Systeme darstellen. Ein Vertreter dieser Systeme ist
das inverse Pendel [1, 2, 3, 4, 5, 6], bei dem ein Pendelstab senkrecht nach oben
zeigend balanciert wird.
Ziel dieser Diplomarbeit war es, einen in der Entwicklungsphase befindlichen Versuchsaufbau fertigzustellen und eine Echtzeit-Regelung zu programmieren, die ein balancierendes Positionieren des
Pendelstabes ermöglicht. Dazu war eine Analyse der physikalischen Zusammenhänge nötig, die zu der Entwicklung eines mathematischen Modells führte. Mit Hilfe dieses Modells konnte der Ablauf der
Regelung simuliert werden.
Die Fertigstellung des Versuchsaufbaues erwies sich als sehr aufwendig, da die Regelung hohe Ansprüche an die Genauigkeit der Meßwerte stellt. Hinzu kam die Tatsache, daß der eingesetzte
Servoverstärker sich als eine Quelle starker Störsignale erwies. Beide Umstände führten dann zu einem Neuentwurf der meßtechnischen Komponenten.
Nachdem ebenfalls einige Schwachstellen in der Mechanik des Versuchsaufbaues beseitigt waren, wurde mit der Entwicklung der Regelungssoftware begonnen. Der implementierte Zustandsregler
ermöglicht ein Positionieren des Pendelwagens bei gleichzeitigem Balancieren des nach oben gerichteten Pendelstabes. Durch diese Arbeit wurde die Grundlage für einen neuen Laborversuch und die
Verwirklichung weiterführender Diplomarbeiten geschaffen.
2 Aufgabenstellung
Die Aufgabenstellung gliedert in sich in zwei Teile, von denen sich der erste mit der Fertigstellung des Versuchsaufbaues befaßt. Hierbei geht es vornehmlich um die Aufnahme und Aufbereitung der
für die Regelung benötigten Meßwerte und ihre Übertragung an den Prozeßrechner. Daneben spielt die Endabschaltung eine große Rolle; sie soll gewährleisten, daß der Pendelwagen den zulässigen
Verfahrbereich nicht verläßt. Im übrigen gehören zu diesem ersten Teil alle elektrischen Installationen, die nötig sind, um den Versuchsaufbau mit dem Prozeßrechner zu steuern.
Der zweite Teil der Aufgabenstellung umfaßt die Analyse des inversen Pendels sowie den Entwurf eines Zustandsreglers und seine Implementierung in Form einer Regelungssoftware. Für die Analyse und
Simulation stehen die Programme MatLab, WinFACT und PASCOS zur Verfügung. Als Programmiersprache kommt Borland Pascal unter Verwendung von RTKernel zum Einsatz.
3 Fertigstellung Versuchsaufbau
3.1 Ausgangsposition
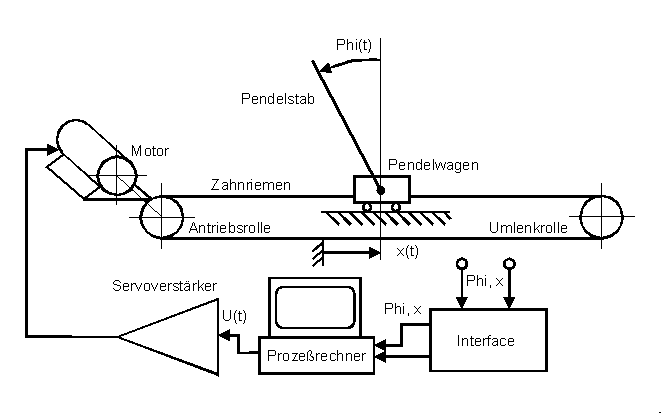
Vor der Fertigstellung bestand der Versuchsaufbau aus dem Gleichstrommotor, versorgt und drehzahlgeregelt von einem Servoverstärker, und dem Pendelwagen mit Pendelstab, befestigt mit einem
Schlitten auf der Gleitschiene. Die Steuerung des Servoverstärkers erfolgte über ein provisorisches Bedienfeld. Aufgebaut waren diese Komponenten auf einem Tisch, wobei der Servoverstärker in
einem Fach unterhalb der Tischplatte untergebracht wurde.
Der Prozeßrechner war mit einer PC-Lab-Karte vom Typ PCL812PG ausgerüstet. Diese Karte besitzt je 16 digitale Ein- und Ausgänge, 16 analoge Eingänge und 2 analoge Ausgänge. Zur Ansteuerung dieser
Karte existierte eine in PASCAL programmierte Unit.
3.2 Sollwertverstärkung
Der Servoverstärker regelt die Drehzahl des Gleichstrommotors entsprechend des Sollwertes, der ihm vorgegeben wird. Die Eingangssollwertspannung des Servoverstärkers liegt zwischen 0 (Motor
steht) und ±10 Volt (maximale Drehzahl links/rechts). Da die Ausgangsspannung der PC-Lab-Karte zwischen 0 und +5 Volt liegt, wurde eine Sollwertverstärkung entwickelt.
Die Schaltung besteht aus zwei Operationsverstärkern, von denen der erste zu der Ausgangsspannung der PC-Lab-Karte eine Spannung von -2.5 Volt addiert. Dadurch verschiebt sich der
Spannungsbereich von 0 bis 5 Volt zu -2.5 bis +2.5 Volt. Diese Spannung wird nun vom zweiten Operationsverstärker um den Faktor 4 verstärkt. Somit kann der volle Eingangsspannungsbereich des
Servoverstärkers ausgenutzt werden.
Die Sollwertverstärkung war anfangs auf einer Platine neben dem Servoverstärker aufgebaut, die Spannungsversorgung erfolgte über das Netzteil des Servoverstärkers. Es stellte sich heraus, daß die von diesem Netzteil zur Verfügung gestellten Spannungen von extremen Störsignalen überlagert wurden. Aus diesem Grunde wurde die Schaltung auf die Prototyp-Platine im Prozeßrechner verlegt. Die Spannungsversorgung erfolgt über das Netzteil des Prozeßrechners. Neben einer besseren Spannungsversorgung wurde so auch eine Abschirmung der Schaltung gegenüber Störeinflüssen z. B. vom Versuchsaufbau erreicht.
3.3 Pegelanpassungen
Ein ähnliches Problem wie bei der Sollwertverstärkung ergab sich bei der Anpassung der unterschiedlichen Signalpegel. Die PC-Lab-Karte arbeitet mit TTL/CMOS-kompatiblen Signalpegeln von 0 (Low)
und 5 Volt (High). Der Servoverstärker hingegen erwartet an seinen Steuereingängen Spannungen von 0 und 10 Volt. Der einzige Signalausgang erzeugt keine Pegel, sondern stellt einen
Offener-Kollektor-Ausgang dar, der im Falle eines Servofehlers eine Verbindung zur Masse herstellt und sonst offen ist.
Als einfachste Lösung zur Pegelanpassung wurde ein Baustein mit invertierenden Offener-Kollektor-Treibern verwendet. Doch leider mußte von dieser Möglichkeit wieder Abstand genommen werden. Über
die gemeinsame Masse von Prozeßrechner und Netzteil des Servoverstärker bestand eine galvanische Verbindung dieser beiden Komponenten. Sie führte dazu, daß die Potentialschwankungen des
Netzteiles ungemindert auf den Prozeßrechner übertragen wurden.
Folglich mußte nach einer Lösung gesucht werden, bei der keine galvanische Verbindung zwischen Prozeßrechner und Servoverstärker besteht. In diesem Fall kommt ein Baustein mit vier Optokopplern zum Einsatz. Diese gewährleisten eine potentialfreie Übertragung der Signale. Die Pegelanpassung ist auf der sog. RELOK-Platine zu finden.
3.4 Selbsthalte-Schaltung
Neben der Not-Aus-Funktion besitzt der Servoverstärker eine richtungsabhängige Endabschaltung. Die Not-Aus-Funktion wird über einen Not-Aus-Knopf aktiviert, der als öffnender Schalter fungiert.
Da der Not-Aus-Knopf in der gedrückten Position einrastet, bleibt der Servoverstärker deaktiviert, bis der Not-Aus-Knopf durch Herausziehen wieder entriegelt wird.
Die Endabschaltung wird ebenfalls durch das Öffnen eines Kontaktes ausgelöst, und zwar durch den Pendelwagen. Dieser betätigt beim Verlassen des zulässigen Verfahrbereiches einen Taster, den sog.
Endtaster. Sobald der Endtaster gedrückt ist, wird die Endabschaltung ausgelöst, d. h. der Servoverstärker ignoriert Sollwerte, die den Wagen weiter in Richtung des betroffenen Endtasters bewegen
würden.
Wäre der Endtaster direkt mit dem entsprechenden Eingang des Servoverstärkers verbunden, könnte es zu folgender Situation kommen: Der Pendelwagen überfährt mit hoher Geschwindigkeit den Endtaster
und betätigt ihn dabei. Die Endabschaltung wird ausgelöst und der Wagen angehalten. Dazu wird vom Gleichstrommotor ein Haltemoment aufgebaut. Geschieht dieses nicht schnell genug, könnte es
passieren, daß der Wagen über den Endtaster hinwegfährt. Die Endabschaltung wäre somit wieder inaktiv, und der Wagen führe mit unverminderter Geschwindigkeit weiter.
Es mußte also eine Schaltung entwickelt werden, die aus diesem evtl. sehr kurzen Signal des Endtasters ein dauerhaftes Signal für die Endabschaltung generiert. Hierbei kam eine
Selbsthalte-Schaltung mit zwei Relais zum Einsatz, so daß ein kurzes Betätigen eines Endtasters solange die Endabschaltung aktiviert, bis ein Taster zur Freigabe der Endabschaltung betätigt
wird.
Die Selbsthalte-Schaltung befindet sich auf der RELOK-Platine, die beleuchteten Taster zur Freigabe der Endtaster im Bedienfeld hinter dem Gleichstrommotor. Die Spannungsversorgung erfolgte
anfangs durch das Netzteil des Servoverstärkers. Aus den schon genannten Gründen (störungsbehaftete Spannungen, galvanische Verbindung über gemeinsame Masse), wurde die Spannung zum Erzeugen des
Signals für den Prozeßrechner von seinem Netzteil bezogen.
3.5 Positionsbestimmung Pendelwagen
Die Positionsbestimmung des Pendelwagens erfolgt über einen Inkrementalgeber. Dieser ist am Gleichstrommotor befestigt und mit der Motorachse verbunden. Der optoelektronische Inkrementalgeber
erzeugt auf zwei Kanälen Rechteckimpulse (500 pro Umdrehung), die zueinander um 90 Grad phasenverschoben sind. Zur Positionsbestimmung müssen diese Impulse gezählt werden. Je nach dem, welcher
Kanal den voreilenden Impuls liefert, ist die Zählrichtung vor- oder rückwärts. Der so ermittelte Zählerstand entspricht der Wagenposition. Im ersten Lösungsansatz wurde versucht, die gesamte
Impulsauswertung in einem PLD vom Typ MACH210 der Firma AMD zu integrieren. Die Programmierung des Bausteins erfolgte mit dem Modul PLSyn des Programmes PSpice. Zur Bestimmung der Zählrichtung
wurde ein Zustandsautomat entwickelt, der erkennt, auf welchem Kanal der voreilende Rechteckimpuls vorliegt, und ein entsprechendes Signal für den Zähler erzeugt. Die Auflösung des Zählers ergab
sich aus der Anzahl der Impulse, die maximal für eine Zählrichtung auftreten können.
Zum Zeitpunkt dieser Überlegung erstreckte sich der maximal zulässige Verfahrweg des Pendelwagens über eine Distanz von 1050 mm. Eine Umdrehung des Antriebsmotors bewegt den Wagen um ca. 90 mm.
Daraus folgt, daß der Antriebsmotor knapp 12 Umdrehungen benötigt, um den Wagen einmal den gesamten zulässigen Verfahrweg passieren zu lassen. Da der Impulsgeber bei einer Umdrehung der
Motorachse 500 Impulse liefert, ergibt sich eine maximale Impulsanzahl von 6000. Ein 13-bit-Zähler wäre somit ausreichend, ein 16-bit-Zähler wurde dann in dem MACH210-Baustein integriert. Zum
Einlesen des Zählerstandes wurde der Prozeßrechner mit einer Steckkarte vom Typ WITIO48 der Firma WASCO ausgestattet, die 48 Ein-/Ausgangskanäle besitzt. Sie wurde über eine in PASCAL
programmierte Unit angesprochen, über ein kleines Testprogramm wurde der Zählerstand am Prozeßrechner ausgegeben. Die Ergebnisse waren nicht zufriedenstellend, da der Zähler keine korrekten
Ergebnisse lieferte. Wurde der Pendelwagen von rechts nach links geschoben, ergab sich ein anderer Zählerstand, als wenn der Pendelwagen von links nach rechts geschoben wurde (jeweils über den
gesamten zulässigen Verfahrweg). Die Ursache hierfür läßt sich nicht genau definieren, aber vermutlich war der Zustandsautomat nicht geeignet, die Zählrichtung zu ermitteln. Deshalb wurde für
diesen Teil der Positionsbestimmung ein Baustein vom Typ LS7082 der Firma MEGATRON Bauelemente eingesetzt. Dieser Baustein enthält eine Logik zur Vervielfachung und Richtungserkennung von
Impulsgeber-Signalen. Der MACH210 wurde in seiner Funktionalität auf den 16-bit-Zähler reduziert. Das Ergebnis schien anfangs deutlich verbessert, da der Zähler nun für beide Bewegungsrichtungen
des Pendelwagens gleiche Zählerstände lieferte. Dieses galt allerdings nur für den Fall, daß der Pendelwagen von Hand bewegt wurde. Sobald der Antriebsmotor den Pendelwagen bewegte, traten wieder
Fehler beim Zählen auf.
Es schien ein Zusammenhang zwischen dem Auftreten der Fehler und der Aktivierung des Servoverstärkers zu bestehen. Sobald letzteres der Fall ist, setzt ein hoher Pfeifton ein, da der
Servoverstärker von einem getakteten Netzteil versorgt wird, welches unter starker Belastung diesen Ton erzeugt. Es lag somit die Vermutung nahe, als daß dieses getaktete Netzteil Störungen
hervorrief. Dieses wurde insofern bestätigt, daß eine Analyse der Versorgungsspannungen des Netzteiles mit einem Oszilloskop deutliche Störfrequenzen offenbarte. Es waren deutliche
Spannungsspitzen zu erkennen, die mit einer Frequenz von 8 kHz auftraten, welches der Tonfrequenz des Pfeiftones entspricht.
Dieser Umstand führte zu den schon beschriebenen Änderungen in der Meßelektronik. Bezüglich der Positionsbestimmung des Pendelwagens wurde nun auch der Ort, an dem die benötigten Bausteine
plaziert wurden, einer genaueren Betrachtung unterzogen. Der MACH210 und der LS7082 befanden sich direkt neben dem Servoverstärker und seinem Netzteil, und von diesem erfolgte auch die
Spannungsversorgung. Jetzt sollte das Dekodieren und Zählen der Impulse im Innern des Prozeßrechners erfolgen, da hier stabile und störungsfreie Spannungsversorgungen zur Verfügung stehen und
dieser Bereich gegen Störungen von außen abgeschirmt ist.
Diese Überlegungen führten zum Einsatz einer Prototyp-Platine [7]. Diese 8-bit-Steckkarte stellt eine vollständige Adreßdekodierung und ein großes Lochrasterfeld zur Verfügung.
Sämtliche am PC-BUS anliegenden Spannungen können ebenfalls abgegriffen werden. Die Möglichkeit, Daten direkt über den PC-BUS zu übertragen, legte die Verwendung eines Bausteins vom Typ LS7166
der Firma MEGATRON Bauelemente nahe. Dieser 24-bit-Zähler mit Mikroprozessor-Interface ist ebenso wie der LS7082 für die Auswertung von Inkrementalgeber-Signalen entwickelt.
Die beiden Rechteckimpulse des Inkrementalgebers werden vom LS7166 dekodiert und gezählt, wobei der Zähltakt - wie beim LS7082 - intern verdoppelt oder vervierfacht werden kann. Da selbst bei
einer Vervierfachung der maximale Zählerstand kleiner als 216 ist, wurde von dieser Option Gebrauch gemacht. Dieses führte zu einer Auflösung von 0,045 mm pro Impuls. Das Auslesen des
Zählerstandes und das Rücksetzen des Zählers erfolgt über den PC-Bus durch eine PASCAL-Unit.
Die zuletzt beschriebene Konfiguration - LS7166 auf Prototyp-Platine im Prozeßrechner - arbeitet fehlerfrei, auch wenn das Netzteil des Servoverstärkers belastet wird. Die Positionsbestimmung des
Pendelwagens ist störungsunempfindlich und hochauflösend.
3.6 Positionsbestimmung Pendelstab
Bei der Positionsbestimmung des Pendelstabes wurde auf eine Technik zurückgegriffen, die schon bei anderen Versuchsaufbauten des Prozeßlabors angewendet wurde. Zur Messung des Winkels wird ein
Präzisionspotentiometer eingesetzt, das über eine Kupplung mit der Pendelachse verbunden ist. Um eine Meßgröße zu erhalten, die mit dem Prozeßrechner aufgenommen werden kann, werden dem
Potentiometer +5 und -5 Volt zugeführt. Am Abgriff des Potentiometers liegt somit je nach Stellung des Pendelstabes eine Spannung zwischen -5 und +5 Volt an. Dieses entspricht dem
Eingangsspannungsbereich der PC-Lab-Karte.
Die beiden Spannungen (±5 Volt) werden durch Spannungsstabilisatoren (78L05/79L05) erzeugt. Diese befinden sich zusammen mit einem einfachen RC-Glied (Tiefpaß zur Meßwertfilterung) und einem
Operationsverstärker (Spannungsfolger zur Meßwertverstärkung) auf einer Platine direkt hinter dem Potentiometer. Die komplette Apparatur (Potentiometer und Meßelektronik) ist gekapselt und
isoliert am Pendelwagen befestigt.
Auch hier stellte die Spannungsversorgung ein großes Problem dar. Sie erfolgte anfangs über das Netzteil des Servoverstärkers. Dieses führte zu extremen Störungen auf dem Meßwertsignal, vor allem
bei Belastung des Servoverstärkers. Aus diesem Grund wurde die Spannungsversorgung vom Prozeßrechner übernommen; so konnte auch eine galvanische Kopplung vermieden werden.
3.7 Spannungsversorgung
Alle oben angeführten Komponenten benötigen Versorgungsspannungen und Massepotentiale. Hierfür schien die Buchse 5 des Servoverstärker-Netzteils geeignet zu sein, da diese alle benötigten
Spannungen zur Verfügung stellt. In der Praxis traten allerdings zwei Probleme auf. Zum einem waren - wie schon erwähnt - die Spannungen des Netzteils von Störfrequenzen überlagert, welches zu
Fehlfunktionen und Meßfehlern bei den oben aufgeführten Komponenten führte.
Das zweite Problem war die elektrische Kopplung von Prozeßrechner und dem Netzteil des Servoverstärkers. Dadurch wurden die Störungen ungemindert auf den Prozeßrechner übertragen. Diese beiden
Punkte führten zu den jeweiligen Neukonzeptionen der Komponenten (z. B. Optokoppler statt Offener-Kollektor-Treiber). Außerdem wurde die Spannungsversorgung vom Prozeßrechner übernommen, da
dieser ebenfalls alle benötigten Spannungen zur Verfügung stellt.
Da sich aber die Spannungsversorgung als extrem wichtiger Faktor sowohl bei der Sollwertverstärkung, als auch bei der Meßelektrik zur Positionsbestimmung des Pendelstabes erwiesen hatte, wurde
ihr diesmal mehr Beachtung geschenkt. Auch die vom Netzteil des Prozeßrechners erzeugten Spannungen erwiesen sich nicht als völlig störungsfrei. Deshalb wurden auf der Prototyp-Platine zwei Arten
von Spannungsfiltern aufgebaut. Der erste besteht aus einem einfachen LC-Glied und bietet eine gute Filterung bei geringem Spannungsabfall. Er wurde zur Filterung der Versorgungsspannungen (±12
Volt) für die Sollwertverstärkung eingesetzt. Die zweite Filterschaltung ist etwas aufwendiger (Transistor, Widerstand, zwei Kondensatoren) und hat einen relativ großen Spannungsabfall (ca. 1
Volt). Dafür findet hier eine sehr starke Filterung statt. Sie kommt bei den Versorgungsspannungen für die Meßelektrik der Positionsbestimmung Pendelstab zum Einsatz.
3.8 Elektrische Verbindungen
Die elektrische Verbindung von Prozeßrechner und Versuchsaufbau bestand anfangs aus zwei 25-poligen Kabeln. Eines diente zur Übertragung des Zählerstandes (Positionsbestimmung Pendelwagen)
während das andere die übrigen Signalleitungen (analog/digital) enthielt. Als der Zähler für die Positionsbestimmung des Pendelwagens in den Prozeßrechner verlegt wurde, war das erste Kabel
hinfällig.
Weitere Überlegungen führten zu dem Schluß, daß die elektrischen Verbindungen gegen Störeinflüsse von außen abgeschirmt sein sollten und für jede Signalgruppe ein eigenes Kabel verwendet werden
sollte. Die Umsetzung erfolgt in Form von vier abgeschirmten Kabelleitungen:
- Kabel: Meßelektrik Winkelgeber, versorgt diese mit +11 und -11 Volt. Das Meßwertsignal wird der PC-Lab-Karte zugeführt. Massepotential ist die Analog-Masse der PC-Lab-Karte.
- Kabel: Impulsgeber, versorgt ihn mit +5 Volt. Die beiden Rechtecksignale (Kanal A und B) werden dem Zählerbaustein zugeführt. Massepotential ist die Masse des Prozeßrechners.
- Kabel: Sollwert, liefert den Sollwert für den Servoverstärker. Massepotential ist die Analog-Masse der PC-Lab-Karte.
- Kabel: Digital-In/Out, versorgt die RELOK-Platine mit +5 Volt zur Erzeugung der High-Pegel (innere Endtaster, Selbsthalteschaltung). Überträgt alle digitalen Signale zwischen Prozeßrechner und Versuchsaufbau. Massepotential ist die Digital-Masse der PC-Lab-Karte.
Alle Kabel besitzen einen Schirm, der mit dem Gehäuse des Prozeßrechners verbunden ist. Auf Steckverbindungen wurde - so weit möglich - verzichtet.
3.9 Einbau der Steuereinheit
Die Steuereinheit, bestehend aus Servoverstärker, Netzteil und der RELOK-Platine, wurde in dem Fach unterhalb der Tischplatte des Versuchsaufbaues eingebaut. Dazu wurde das Gehäuse mit einem Aluminiumwinkel mit der Bodenplatte verschraubt. Der Netztransformator wurde ebenfalls fest mit dem Versuchsaufbau verschraubt. Sämtliche Komponenten wurden über den Erdungsanschluß des Transformators geerdert.
4 Modifikation des Versuchsaufbaues
4.1 Spannvorrichtung Zahnriemen
Als eine Steuerung des Versuchsaufbaues möglich war, wurde schnell klar, daß eine Modifikation nötig war. Bei plötzlichen Änderungen des Stellwertes kam es zu einem Überspringen des Zahnriemens
am Antriebsrad, und zwar dann, wenn der Pendelwagen sich vom Antriebsmotor wegbewegen sollte. In dieser Situation muß der Zahnriemen vom Antriebsrad quasi weggedrückt werden. Dadurch hebt dieser
sich vom Antriebsrad ab und es dreht unter dem Zahnriemen durch.
Die Ursache für dieses Überspringen war schnell gefunden. Der Zahnriemen war nicht straff genug gespannt und ließ sich mit den dafür vorgesehenen Zahnrädern unterhalb der Gleitschiene nicht
ausreichend spannen. Es wurde eine Spannvorrichtung entworfen, mit der sich der Zahnriemen mit einfachen Mitteln straff spannen läßt. Nachdem diese Spannvorrichtung die Umlenkrolle am Ende der
Gleitschiene ersetzt hatte und der Zahnriemen entsprechend gespannt war, kam es zu keinem Überspringen mehr.
Die vorher für das Spannen des Zahnriemens vorgesehenen Zahnräder erwiesen sich fortan als störend, da sie nur unzureichend gelagert waren. Sie wurden entfernt.
4.2 Neuer Pendelwagen
Im Laufe der Fertigstellung des Versuchsaufbaues erwies sich der Pendelwagen als nicht ausreichend bezüglich seiner Konstruktion. Mängel in der Lagerung der Achse, an der der Pendelstab befestigt
war, führten zu Meßfehlern. Da sich das Netzteil des Servoverstärkers als eine Quelle elektrischer Störsignale erwiesen hatte, schien auch eine Kapselung der auf dem Pendelwagen befindlichen
Meßelektrik sinnvoll.
Aus diesen Gründen wurde ein komplett neuer Pendelwagen konstruiert, diesmal unter dem Gesichtspunkt einer spielfreien Lagerung der Pendelachse und der Kapselung der Meßelektrik. Auch der
Stabilität wurde eine große Bedeutung zugemessen. Aus diesem Grunde wurde der Pendelstab, der vorher aus einem Messingstab mit 10 mm Durchmesser bestand, durch ein Rechteckprofil (10x20 mm) einer
Aluminiumlegierung ersetzt. Für spätere Stabilitätsuntersuchungen der Regelung wurde an dem Pendelstab ein Winkel als Auflagefläche befestigt.
5 Systemanalyse und Reglerentwurf
5.1 Zustandsraum-Darstellung
Bei der Zustandsraum-Darstellung werden lineare Systeme n-ter Ordnung in n Teilsysteme erster Ordnung zerlegt, um die mathematische Beschreibung und den Entwurf des Zustandsreglers übersichtlich
zu gestalten [6]. Bei dem inversen Pendel handelt es sich um ein Mehrgrößensystem mit vier Zustandsgrößen, da es ebenso viele wesentliche Speicherfunktionen hat. Je zwei dieser
Zustandsgrößen beziehen sich auf den Pendelwagen und auf den Pendelstab. Beide Systeme für sich betrachtet stellen eine zweifach integrierende Strecke dar. Sie sind miteinander gekoppelt, da eine
Bewegung des Pendelwagens auch immer eine Bewegung des Pendelstabes nach sich zieht. Die Rückwirkung der Bewegungen des Pendelstabes können hier vernachlässigt werden, da der Servoverstärker die
daraus resultierenden Bewegungen des Pendelwagens verhindert.
Der Reglerentwurf baut auf der mathematischen Beschreibung auf, die durch die Systemanalyse von dem Mehrgrößensystem gewonnen wurde. Die Differentialgleichungen werden in Matrix- und Vektorform
gebracht und können fortan durch Matrixoperationen umgewandelt werden. Deshalb empfiehlt sich an dieser Stelle der Einsatz von MatLab. Man erhält letztlich die Eigenwerte des Systems, an denen in
diesem Fall die Instabilität des Systems erkennbar ist. Bei der hier verwendeten Methode der Polvorgabe wird - basierend auf neuen, gewählten Eigenwerten - ein Wunschsystem geschaffen, welches
ein stabiles Verhalten besitzt. Die Differenz zwischen dem realen, instabilen System und dem Wunschsystem wird dann von dem Zustandsregler mit Hilfe der errechneten Regelerkoeffizienten
aufgebracht.
Die Aufgabe des Zustandsreglers besteht darin, aus den Zustandsgrößen und dem Sollwert die Stellgröße zu errechnen. Dabei werden die Zustandsgrößen mit konstanten Reglerfaktoren und der Sollwert
mit dem Vorfilterwert multipliziert. Die Summe dieser Produkte ist dann die gesuchte Stellgröße. Man könnte vereinfacht von vier überlagerten P-Reglern sprechen. Daran ist sofort zu erkennen, daß
der Zustandsregler keine I- oder D-Anteile besitzt. Letztere sind nur insofern vorhanden, als daß eine Zustandsgröße das Differential einer anderen Zustandsgröße sein kann. Somit fließen dann
wiederum D-Anteile in die Regelung mit ein.
5.2 Systemanalyse
Bei der Systemanalyse und dem Reglerentwurf wurde die Vorgehensweise von Zirpel [6] übernommen. Seine Ausführungen beziehen sich auf einen Versuchsaufbau der Hochschule Bremen
mit ähnlichen Eigenschaften wie der in dieser Arbeit beschriebene.
Die von Zirpel genannten Voraussetzungen sind erfüllt: Die Geschwindigkeit des Pendelwagens (Wagengeschwindigkeit) ist proportional zur Stellgröße y. Die Wagengeschwindigkeit reagiert auf ein
sprungförmige Stellgrößenänderung mit einem PT1-Verhalten. Und die Rückwirkungen der Last auf den Bewegungsablauf des Pendelwagens dürfen vernachlässigt werden. Die Einhaltung dieser
Voraussetzungen gewährleistet der Servoverstärker.
Zuerst wird das linearisierte Prozeßmodell vierter Ordnung beschrieben. Die vier Zustandsgrößen werden folgendermaßen festgelegt:
- Zustandsgröße q0: Wagenposition x, ermittelt von der Positionsbestimmung Pendelwagen
- Zustandsgröße q1: Wagengeschwindigkeit x', durch numerische Ableitung:
- Zustandsgröße q3: Pendelposition Alpha, ermittelt von der Positionsbestimmung Pendelstab
- Zustandsgröße q4: Pendelgeschwindigkeit Alpha', durch numerische Ableitung:
Zur Simulation des Prozesses und der Auslegung des Zustandsreglers werden nur drei Prozeßwerte benötigt:
- K: Proportionalitätsfaktor zwischen Stellgröße y und Wagengeschwindigkeit x'.
- T: Zeitkonstante des PT1-Gliedes, das den Servoverstärker repräsentiert.
- l: Länge des Pendelstabes als Schwerpunktsabstand.
Wie schon erwähnt, läßt sich die Übergangsfunktion der Drehzahl mit der eines PT1-Gliedes annähern. Somit ist die Übergangsfunktion der Wagengeschwindigkeit:
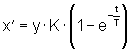 (1)
(1)
Die Ableitung von (1) ergibt die Wagenbeschleunigung:
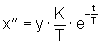 (2)
(2)
Eliminiert man nun e-t/T aus (2), so erhält man die Differentialgleichung für den Pendelwagen:
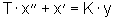 (3)
(3)
Veranschaulicht wird dieses, indem (3) nach x'' aufgelöst wird und als Signalflußplan (SFP) dargestellt wird (Abb. 1: SFP Pendelwagen).
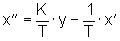 (4)
(4)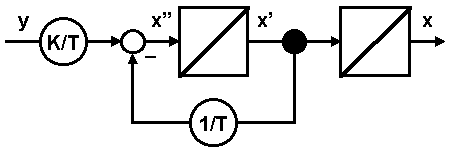
Abb. 1: SFP Pendelwagen
| Als nächstes wird der Bewegungsablauf des Pendelsystems untersucht. Auf das hängende Pendel (Abb. 2: Hängendes Pendel) wirken zwei Kräfte: Die nach unten gerichtete Gewichtskraft FG und die Stabkraft FS. Letztere überträgt die Bewegungen des Pendelwagens auf die Last L (Schwerpunkt des Pendelstabes). Die Lastmasse m entspricht der Masse des Pendelstabes. |
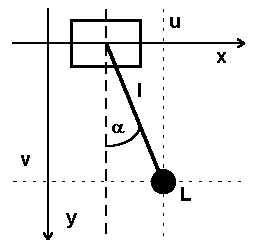 Abb. 2: Hängendes Pendel |
Damit ergeben sich Bilanzen der Horizontal- und Vertikalkräfte, deren Summen nach dem Newtonschen Kräftegleichgewicht jeweils den Wert Null ergeben müssen.
Horizontalkräfte:
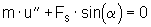 (5)
(5)
Vertikalkräfte:
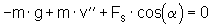 (6)
(6)
Für die Zustandsgleichungen, in denen nur q0, q1, q2 und q3 enthalten sind, müssen alle anderen Variablen (FS, u und v) eliminiert werden.
Erweitert man (5) mit cos(Alpha) und (6) mit sin(Alpha), so erhält man:
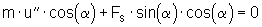 (5a)
(5a)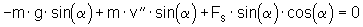 (6a)
(6a)
Zieht man (6a) von (5a) ab, wird die Stabkraft FS entfernt. Anschließend wird das Ergebnis durch die Lastmasse m dividiert und diese so ebenfalls entfernt:
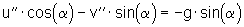 (7)
(7)
Die Koordinaten der Last (u und v) werden mit Hilfe der Transformationsgleichungen eliminiert:
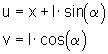 (8)
(8)
Da die Variablen u und v in ihrer zweiten Ableitung in (7) auftreten, müssen Sie zweimal abgeleitet werden:
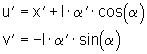 (9)
(9)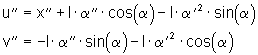 (10)
(10)
Die Gleichungen für u'' und v'' (10) werden in (7) eingesetzt. So erhält man die nichtlineare Differentialgleichung des Pendelsystems:
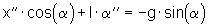 (11)
(11)
Um diese Differentialgleichung zu linearisieren, wird der Pendelwinkel Alpah als sehr klein angenommen:
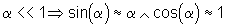
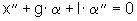 (12)
(12)
Die linearisierte Differentialgleichung (12) wird nach a'' aufgelöst und als SFP dargestellt (Abb. 3: SFP Pendelstab):
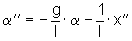 (13)
(13)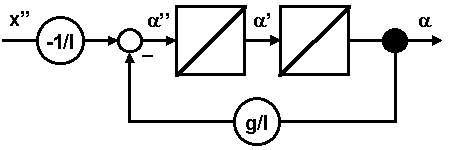
Abb. 3: SFP Pendelstab
Für x'' in der Zeitgleichung für das Pendelsystem (13) kann die Zeitgleichung für den Pendelwagen (4) eingesetzt werden. Dieses ermöglicht die Verknüpfung der Signalflußpläne (Abb. 4: SFP Lastkran):
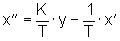 (4)
(4)eingesetzt in
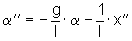 (13)
(13)ergibt
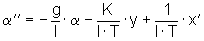 (14)
(14)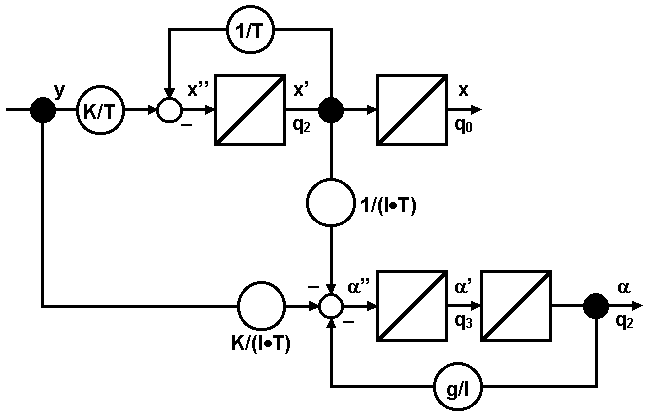
Abb. 4: SFP Lastkran
Um das System im Zustandsraum zu beschreiben, werden die linearen Differentialgleichungen in Zustandsgleichungen umgewandelt. Hierfür werden die Variablen x, x', Alpha und Alpha' durch die Zustandsgrößen q0, q1, q2 und q3 ersetzt:
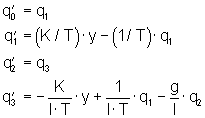 (15)
(15)
Für die übersichtliche Kurzform werden Vektoren und Matrizen eingeführt. Man erhält die Vektor-Differentialgleichung für Zustandsgrößen:
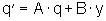 (1)
(1)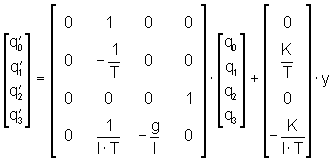 (1)
(1)
Da Zustandsgrößen und Ausgangsgrößen übereinstimmen, wird die Vektor-Gleichung für die Ausgangsgrößen nicht benötigt.
| Das Prozeßmodell für das System mit nach oben gerichtetem Pendelstab (Abb. 5: Stehende Last) ist dem eben beschriebenen sehr ähnlich. Die Differentialgleichung für den Pendelwagen ändert sich nicht. Die Tatsache, daß der Nullpunkt des Pendelwinkels sich um 180 Grad verschoben hat, findet dadurch Beachtung, daß in der Differentialgleichung für das nach unten gerichtete Pendelsystem Alpha durch Beta-PI ersetzt wird. |
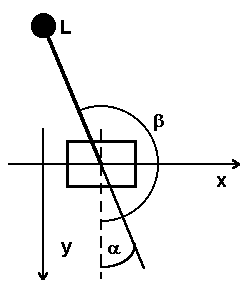 Abb. 5: Stehende Last |
Demzufolge gelten folgende Gleichungen:
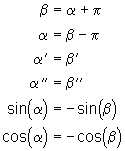 (17)
(17)
Zur Erinnerung hier noch einmal die Differentialgleichung für das Pendelsystem mit der Last unten:
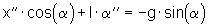 (11)
(11)
Setzt man die oben aufgeführten Gleichungen (17) ein, so erhält man die Differentialgleichung für das Pendelsystem mit der Last oben:
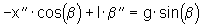 (18)
(18)
Diese wird ebenfalls linearisiert:
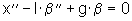 (19)
(19)
Zusammen mit der unveränderten Differentialgleichung für den Pendelwagen ergibt sich die Differentialgleichung für das komplette System zu:
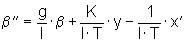 (20)
(20)
Wieder werden den Prozeßgrößen Zustandsgrößen zugeordnet:
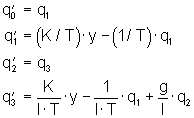 (21)
(21)
Ebenso erfolgt die übersichtliche Kurzform durch die Einführung von Vektoren und Matrizen:
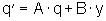 (22a)
(22a)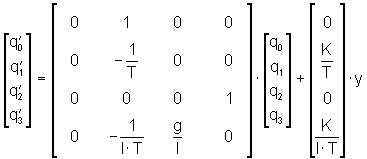 (22b)
(22b)
Da auch hier Zustandsgrößen und Ausgangsgrößen übereinstimmen, wird die Vektor-Gleichung für die Ausgangsgrößen wieder nicht benötigt.
5.3 Ermittlung der Prozeßparameter mit WinFACT
Für den anschließenden Reglerentwurf werden die Prozeßparameter benötigt:
- Zeitkonstante des Servoverstärkers (T)
- Verstärkung des Servoverstärkers (K)
- Länge des Pendelstabes als Schwerpunktabstand (l)
Die Länge des Pendelstabes wurde in Auspendelversuchen gemessen. Um die Parameter des Servoverstärkers zu ermitteln, wurde mit der Windows-Software WinFACT folgende Steuerung entwickelt (Abb. 6: Blocksystem zur Identifikation des Servoverstärkers).
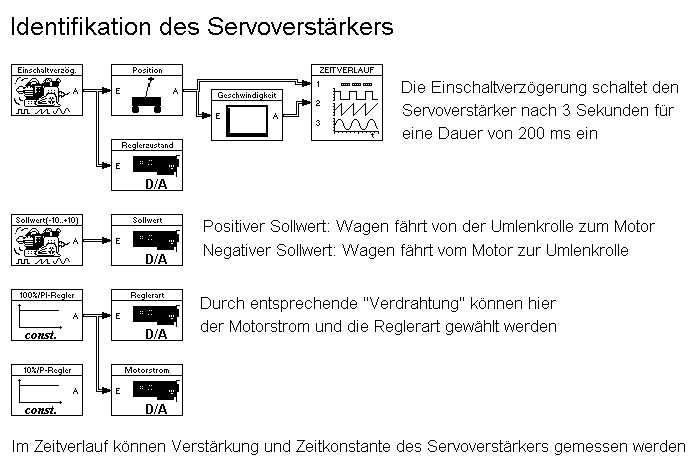
Abb. 6: Blocksystem zur Identifikation des Servoverstärkers
Für verschiedene Sollwertsprünge (von 0 auf 1 bis 10 Volt in 1 Volt-Schritten) ergaben sich folgende Kurvenverläufe der Wagengeschwindigkeit (Abb. 7: Sprungantworten des Servoverstärkers).
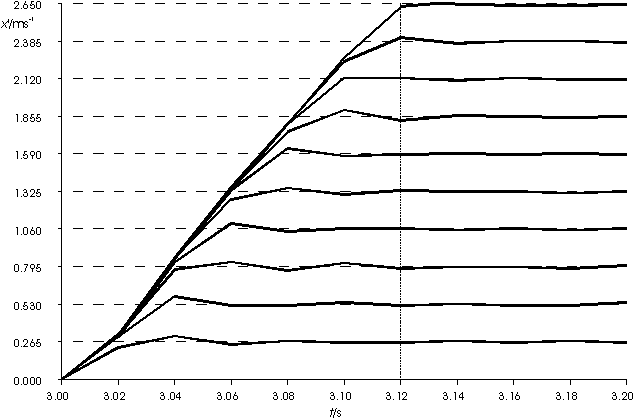
Abb. 7: Sprungantworten des Servoverstärkers
Deutlich ist zu erkennen, daß der Servoverstärker die Soll-Geschwindigkeit mit einer konstanten Beschleunigung zu erreichen versucht. Dieses führt dazu, daß niedrige Geschwindigkeiten schneller
erreicht werden als höhere. Als Zeitkonstante für den Servoverstärker wurde schließlich der größtmögliche Wert angenommen (T = 0,12 s). Aus den Kurvenverläufen läßt sich ebenfalls die Verstärkung
ablesen (K = 0,265 m/sV).
Beide Werte gelten nur, wenn der Servoverstärker durch die entsprechenden Steuersignale dazu aufgefordert wird, intern einen PI-Regler zur Drehzahlregelung zu verwenden, und dabei mit dem vollen
Motorstrom zu arbeiten. Jede andere Kombination der Steuersignale, die die Verwendung eines P-Reglers und/oder Einsatz von nur 10 % des normalen Motorstromes ergibt, führt zu einem schlechteren
bis unbrauchbaren Verhalten des Servoverstärkers.
5.4 Reglerentwurf
5.4.1 Weg-Regelung
Es findet eine reine Positionsregelung statt. Dabei wird die Regeldifferenz (Differenz von Soll-Position und Ist-Position) mit einem konstanten Faktor multipliziert und dieser Wert als Stellgröße
auf den Servoverstärker gegeben. Es handelt sich hierbei also um einen P-Regler.
Als Verstärkung des P-Reglers wurde der Wert 10 gewählt, da die maximale Regeldifferenz 0,8 m beträgt. Wird diese mit dem Faktor 10 multipliziert, so ergibt sich eine Stellgröße von 8 Volt. Also
ein Wert, den der Servoverstärker umsetzen kann.
Beim Positionieren des Pendelwagens kommt es zu einem unerwünschten Schwingen des Pendelstabes. Aus diesem Grunde wurde als nächstes eine Lastkran-Regelung entwickelt, die ein pendelfreies
Positionieren ermöglicht.
5.4.2 Lastkran-Regelung
Für die Lastkran-Regelung wird ein Zustandsregler eingesetzt, der das ungedämpfte Realsystem (im folgenden mit "alt" bezeichnet) in ein ausreichend gedämpftes Wunschsystem ("neu") umwandelt.
Dafür werden zunächst Zahlen in die Eingangs- und Systemmatrix eingesetzt: T = 0,12; K = 0,265; l = 0,465.
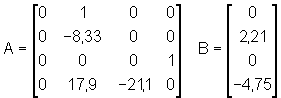
Für den Entwurf des Zustandsreglers wird das zu regelnde System in die Regelungs-Normalform (RNF) überführt. In einem Zwischenschritt wird hierfür die Transformationsmatrix TN berechnet, und zwar mit Hilfe eines von Zirpel zur Verfügung gestellten MatLab-Programmes (zr2tn):
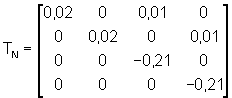
Die Systemmatrix in RNF (AN) läßt sich nun sehr einfach berechnen:
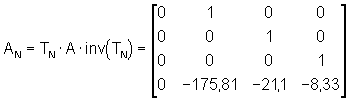
Die charakteristischen System-Eigenwerte für das Realsystem lauten:
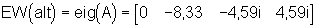
An der dritten und vierten Imaginärlösung laßt sich deutlich erkennen, daß es sich bei dem Realsystem um ein ungedämpftes Schwingsystem handelt.
Um zu dem pendelfreien Wunschsystem zu gelangen, wird letzteres durch die Vorgabe seiner Eigenwerte definiert. Es werden also die Pole des Systems vorgegeben (Polvorgabe). Die Pole müssen dabei
so plaziert werden, daß der Stellbereich des Servoverstärkers nicht verlassen wird. Obwohl das von Zirpel beschriebene System in seinen Eigenschaften nicht mit dem hier beschriebenen
übereinstimmt, wurden zunächst die von ihm gewählten Pole des aperiodischen Wunschsystems übernommen:
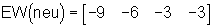
Diese Pole erwiesen sich als sehr günstig, denn sämtliche Reglerentwürfe mit andere Polvorgaben lieferten nur schlechtere Ergebnisse.
Mit Hilfe eines weiteren von Zirpel gelieferten MatLab-Programmes (eig2rnf) läßt sich aus den neuen Eigenwerten die neue Systemmatrix in RNF berechnen:
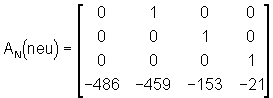
Der vom Zustandsregler aufzubringende Teil ergibt sich aus der Differenz von AN(neu) und AN(alt):
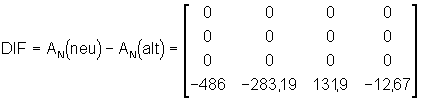
Die Koeffizienten des Zustandsreglers RN in der RNF stehen in der letzten Zeile der Differenzmatrix:
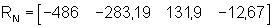
Diese Koeffizienten müssen noch aus der RNF in die Originalform zurücktransformiert werden:
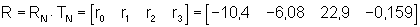
Der Zustandsregler besteht zusätzlich zu den vier Koeffizienten aus einem sog. Vorfilterwert im Sollwertkanal. Dieses Korrekturglied stellt sicher, daß im stationären Ruhezustand der Sollwert (w)
und der Istwert (x) betragsgleich sind
Die Berechnung erfolgt aus der Anschauung: Im stationären Zustand sind alle Integrierer-Eingangssignale und die Stellgröße gleich null. Der Vorfilterwert muß nun dafür Sorge tragen, daß folgende
zwei Gleichungen erfüllt sind:
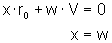
Dieses ist genau dann der Fall, wenn V gleich -r0, also 10,4 ist.
5.4.3 Balance-Regelung
Bei der Balance-Regelung wird der Pendelstab von Hand in eine senkrecht nach oben gerichtete Position gebracht. Die Regelung sorgt nach dem Loslassen dafür, daß der Pendelstab balanciert wird und
dabei positioniert werden kann.
In die Eingangs- und Systemmatrix werden die ermittelten Prozeßparameter eingesetzt:
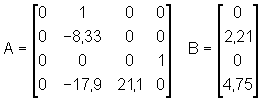
Da der Ablauf zur Ermittlung der Reglerkoeffizienten bekannt ist, wird hier auf die Herleitung verzichtet. Sie lauten:
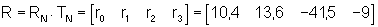
Der Vorfilter errechnet sich analog und hat den Wert -10,4.
6 Software
6.1 Simulation
6.1.1 Weg-, Lastkran- und Balance-Regelung mit WinFACT
Um die verschiedenen Regelungen unter WinFACT simulieren zu können, wurde zunächst das Prozeßmodell des Lastkran-Systems als Superblock (Abb. 8: Lastkran-Modell als Superblock) definiert:
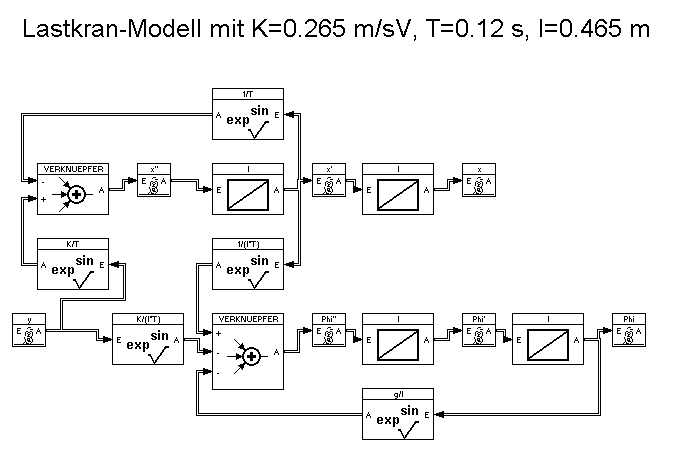
Abb. 8: Lastkran-Modell als Superblock
Das Prozeßmodell für das Balance-System unterscheidet sich von dem oben abgebildeten in einigen umgekehrten Vorzeichen. Obwohl es theoretisch möglich wäre, die beiden Geschwindigkeiten (Wagen und
Pendel) nach außen zu führen, wird von dieser Möglichkeit kein Gebrauch gemacht. Denn in der Realität sind diese beiden Zustandsgrößen nicht direkt meßbar. Der Superblock besitzt somit einen
Eingang (Stellgröße) und zwei Ausgänge (Wagen- und Pendelposition).
Für die Simulation der Weg-Regelung (Abb. 9: Blocksystem zur Simulation der Weg-Regelung) wird ein Generator zu Sollwertvorgabe verwendet, der einen Sollwertsprung von 0 m auf 1 m erzeugt. Über
einen Subtrahierer wird die Regeldifferenz (Sollposition - Istposition) gebildet. Diese wird über ein P-Glied mit der V = 10 verstärkt. Die so gewonnene Stellgröße wird auf das Prozeßmodell
gegeben. Die zurückgelieferten Prozeßdaten werden in Form eines Zeitverlaufes und einer Visualisierung optisch dargestellt. Zusätzlich wird für Optimierungszwecke die maximale Stellgröße
ermittelt und angezeigt.
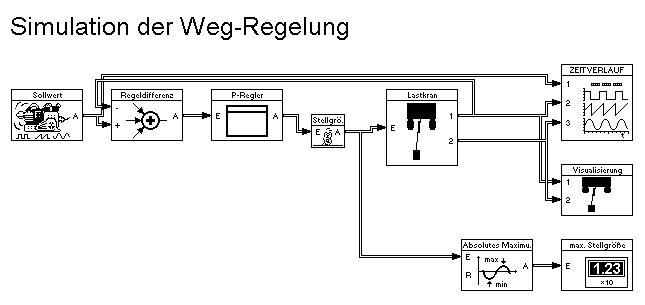
Abb. 9: Blocksystem zur Simulation der Weg-Regelung
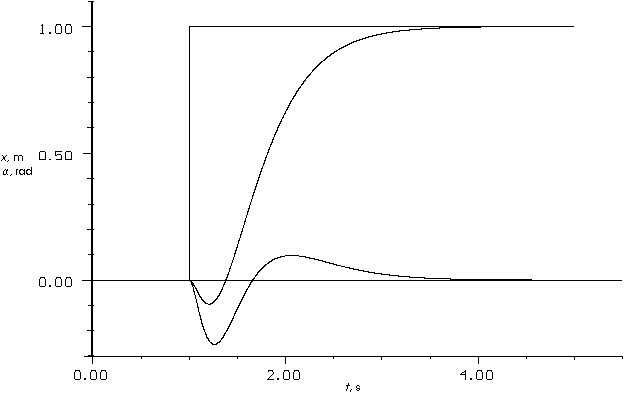
Die drei Größen Sollwert, Wagen- und Pendelposition werden im Folgenden als Kurvenverläufe dargestellt. Das Ergebnis der Simulation (Abb. 10: Kurvenverläufe der mit WinFACT simulierten Weg-Regelung) zeigt deutlich das ungedämpfte Schwingen des Pendelstabes auch nach Erreichen der Sollposition. Um die Prozeßdaten möglichst wirklichkeitsnah zu visualisieren, wurde ein Ausgabeblock programmiert. WinFACT bietet die Möglichkeit, eigene Bildschirmausgaben (Animationen) in Form von DLLs zu implementieren. Basis hierfür waren die mitgelieferten Beispieldateien.
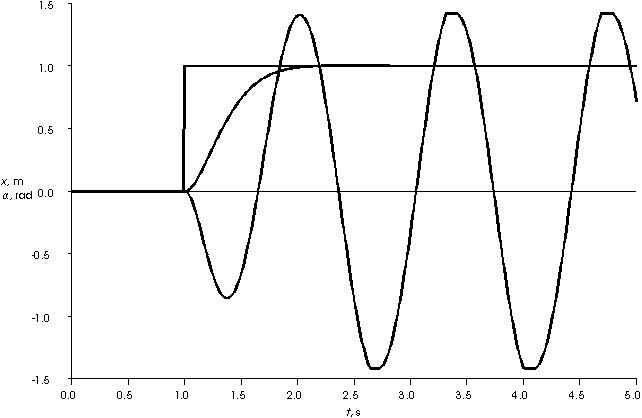
Abb. 10: Kurvenverläufe der mit WinFACT simulierten Weg-Regelung
Für die Simulation der Lastkran- und der Balance-Regelung benötigt der Zustandsregler die Prozeßdaten Pendel- und Wagengeschwindigkeit. Diese werden jeweils durch einen Differenzierer berechnet. Die vier Zustandsgrößen werden dann mit den dazugehörigen Reglerkoeffizienten multipliziert und diese Produkte anschließend summiert. Zu dieser Summe wird der mit dem Vorfilterwert multiplizierte Sollwert addiert; das Ergebnis ist die Stellgröße. Da sich die beide Simulationen sehr ähneln, wird hier nur die der Balance-Regelung (Abb. 11: Blocksystem zur Simulation der Balance-Regelung) dargestellt.
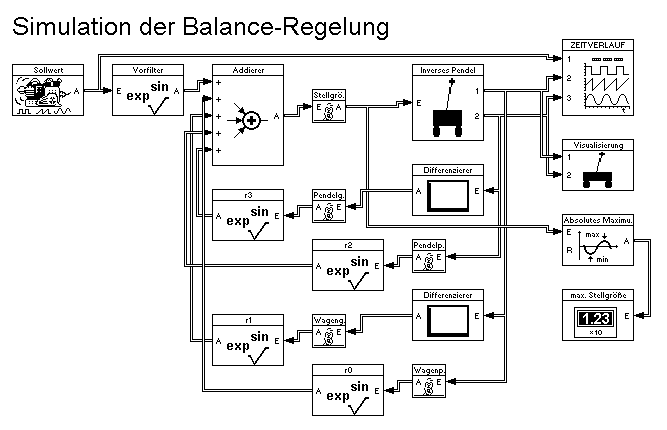
Abb. 11: Blocksystem zur Simulation der Balance-Regelung
Das Simulationsergebnis der Lastkran-Regelung (Abb. 13: Kurvenverläufe der mit WinFACT simulierten Lastkran-Regelung) zeigt deutlich, wie der Pendelwagen kurz nach dem Start seine Geschwindigkeit
verringert. So wird der Pendelstab dazu gebracht, in Richtung der Sollposition zu schwingen. Danach erhöht der Pendelwagen seine Geschwindigkeit wieder etwas, um dann vorsichtig abzubremsen. Wenn
der Pendelwagen die Sollposition erreicht hat, ist der Pendelstab wieder senkrecht nach unten gerichtet und schwingt nicht mehr.
Der Kurvenverlauf der Pendelposition bei der Simulation der Balance-Regelung (Abb. 14: Kurvenverläufe der mit WinFACT simulierten Balance-Regelung) ist identisch mit der oben beschriebenen
Simulation. Der Pendelwagen zeigt ein auf den ersten Blick unverständliches Verhalten: Er bewegt sich für einen kurzen Moment von der Sollposition weg. Der Sinn dieses Vorganges wird deutlich,
wenn man sich das Resultat vor Augen führt.
Vor dem Sollwertsprung befindet sich das System im stationären Zustand. Der Pendelwagen befindet sich an seiner derzeitigen Sollposition und der Pendelstab wird senkrecht nach oben stehend
balanciert. Würde der Pendelwagen sich im Augenblick des Sollwertsprunges direkt zu der angestrebten Position hinbewegen, hätte dieses negativen Folgen. Der Pendelstab würde "nach hinten" kippen,
also zu der von der Sollposition abgewandten Seite. Der Pendelwagen müßte dann umkehren, um den Pendelstab wieder in Balance zu bringen. Aus diesem Grunde fährt der Pendelwagen nach dem
Sollwertsprung einen Augenblick in die "falsche" Richtung (Abb. 12: Prinzip des Balanciervorganges). Dadurch kippt der Pendelstab in Richtung der Sollposition. Nun kann der Pendelwagen dem
Pendelstab quasi hinterherfahren und erreicht so seine Sollposition. Am Ende dieses Vorganges bremst der Pendelwagen so ab, daß der Pendelstab wieder in der senkrecht nach oben gerichteten
Position zum Stillstand kommt.
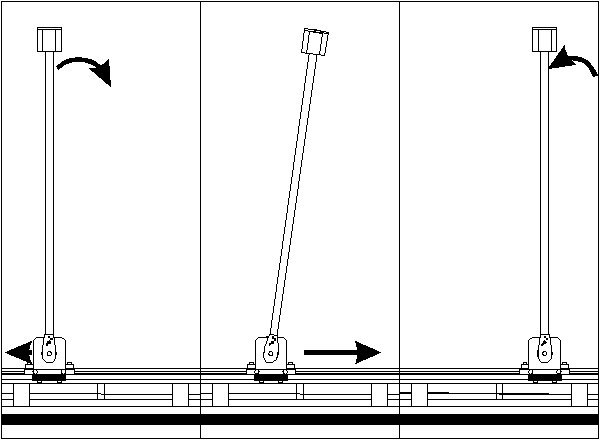
Abb. 12: Prinzip des Balanciervorganges
Abb. 13: Kurvenverläufe der mit WinFACT simulierten Lastkran-Regelung
Abb. 14: Kurvenverläufe der mit WinFACT simulierten Balance-Regelung
6.1.2 Lastkran- und Balance-Regelung mit PASCOS
Für die Simulation der Lastkran- und Balance-Regelung mit PASCOS wurde je ein Programm erstellt. Der Zustandsregler läßt sich hier sehr einfach implementieren, es handelt sich nur um eine Zeile:
y:= Limit( -maxy, maxy, r0*x+r1*xdot+r2*phi+r3*phidot+Vf*w);
Durch die Limit-Funktion wird die Stellgröße begrenzt. Das Prozeßmodell ist in Form eines Makros implementiert. Dieses stellt quasi eine 1:1-Umsetzung des WinFACT-Superblockes dar. Jeder Integrierer in dem Superblock findet sich in dem Makro als Aufruf eines PASCOS-Integrierers wieder:
x:= IntGl( 0, xdot);
Die Simulationsergebnisse sowohl für die Lastkran- (Abb. 15: Kurvenverläufe der mit PASCOS simulierten Lastkran-Regelung) als auch für die Balance-Regelung (Abb. 16: Kurvenverläufe der mit PASCOS simulierten Balance-Regelung) stimmen mit denen von WinFACT überein.
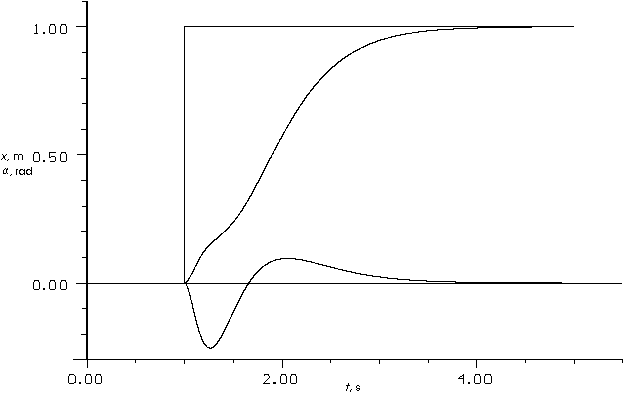
Abb. 15: Kurvenverläufe der mit PASCOS simulierten Lastkran-Regelung
Abb. 16: Kurvenverläufe der mit PASCOS simulierten Balance-Regelung
6.2 Regelung
6.2.1 MatLab-Programme zur Berechnung der Regelparameter
Da sich in der Entwicklungsphase die Prozeßparameter ständig änderten, wurden zwei MatLab-Programme erstellt. Diesen werden als Parameter die drei Prozeßparameter (K, T, l) und die bei der
Polvorgabe zu verwendenden Eigenwerte des Wunschsystems übergeben. Die Programme setzen diese Werte in die Eingangs- und Systemmatrix ein und rufen dann die von Zirpel erstellte Funktion zr2r
auf. Sie liefert dann direkt die vier Reglerkoeffizienten r0 bis r3.
6.2.2 Weg- und Lastkran-Regelung mit WinFACT
Für die Regelung des Versuchsaufbaues mit WinFACT mußten Schnittstellen geschaffen werden, über die WinFACT mit dem Versuchsaufbau kommunizieren kann. Die Ansteuerung der PC-Lab-Karte wird von
WinFACT unterstützt, ein Problem stellte lediglich das Auslesen des Zählerbausteins auf der Prototyp-Platine dar. Die Lösung kam in Form der Beta-Version von WinFACT 96, die sogenannte
USER-Blöcke zur Verfügung stellt. Die Funktionalität eines solchen Blockes wird vom Benutzer selbst in Form einer DLL (Dynamic Linked Library) definiert, die in diesem Fall mit Borland Pascal
programmiert wurde (POSITION.PAS). Aufgabe des für die Regelung verwendeten USER-Blockes "Position" war es, an seinem Ausgang die Wagenposition zur Verfügung zu stellen. Dazu wurde intern der
Zählerbaustein über die PORT-Funktion ausgelesen und der Zählerstand in die entsprechende Position umgerechnet. Der USER-Block besitzt außerdem einen Eingang, über den der Zählerbaustein auf Null
zurückgesetzt werden kann. Dieses muß beim Start der Regelung geschehen. Ebenfalls beim Start muß der Winkeloffset ermittelt werden. Über ein Abtast/Halteglied wird der Winkel zum Startzeitpunkt
eingelesen und gespeichert. Dieser Wert wird fortan von dem gemessenen Winkel abgezogen, so daß die Pendelposition zum Startzeitpunkt einen Winkel von Null Grad repräsentiert.
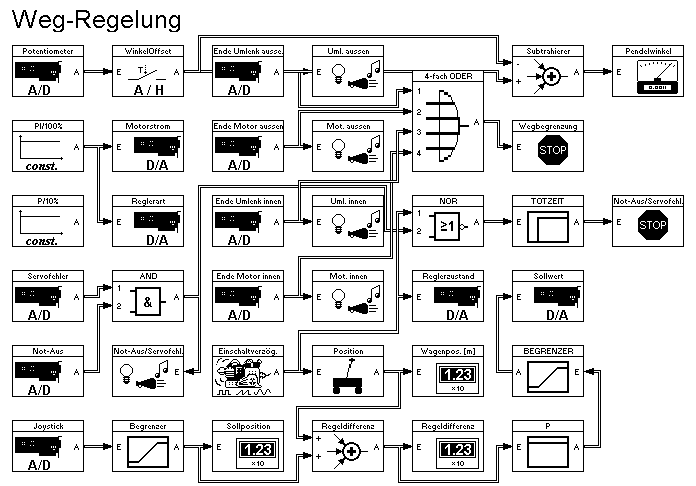
Abb. 17: Blocksystem zur Weg-Regelung mit WinFACT
Da bei der Weg-Regelung (Abb. 17: Blocksystem zur Weg-Regelung mit WinFACT) die Abtastzeit von keiner großen Bedeutung ist, konnte sie sehr groß gewählt werden. Das ermöglicht die Ausgabe der
Prozeßdaten mit Hilfe der von WinFACT zur Verfügung gestellten Anzeige-Blöcke. Es war auch möglich, die verschiedenen Abbruchkriterien zu beachten.
Bei der Lastkran-Regelung (Abb. 18: Blocksystem zur Lastkran-Regelung mit WinFACT) erlaubte die geringe Abtastzeit nur eine sehr geringe Anzahl von Systemblöcken. Aus dem selben Grunde wird die
Sollwertvorgabe, die bei der Weg-Regelung über den Joystick am Prozeßrechner erfolgte, von einem Generator übernommen. Er erzeugt periodische Sollwertsprünge, die den Wagen von links nach rechts
und zurück fahren lassen. Die starken Störungen bei der Messung der Pendelposition erforderten den Einsatz eines PT1-Blockes als Filter 1. Ordnung. Zusätzlich wurde der Stellwert über ein
weiteren PT1-Block geglättet.
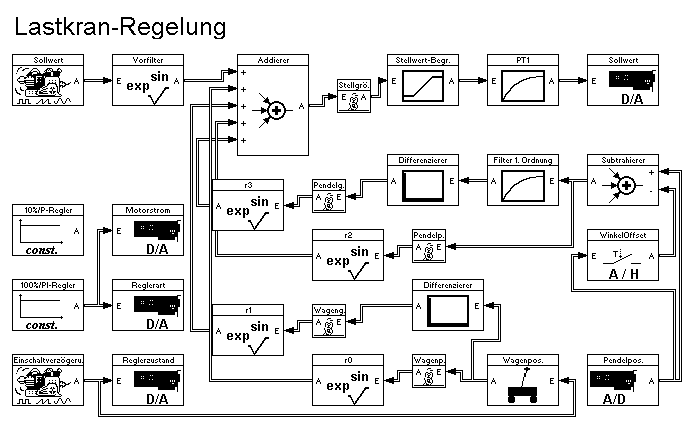
Abb. 18: Blocksystem zur Lastkran-Regelung mit WinFACT
Eine Balance-Regelung mit WinFACT wurde nicht in Betracht gezogen, da die große Dynamik bei dieser Regelung es nicht zuläßt, auf die Beachtung der Abbruchkriterien zu verzichten. Abhilfe würde hier eventuell ein schnellerer Prozeßrechner schaffen, so daß bei der kleinen Abtastzeit eine größere Anzahl von Systemblöcken eingesetzt werden kann.
6.2.3 Weg-, Lastkran- und Balance-Regelung mit Pascal und RTKernel
Die drei Arten der Regelung wurden in einem Programm zusammengefaßt. Es bietet dem Benutzer die Möglichkeit, eine der drei Regelungsarten auszuwählen. Anschließend muß ggf. der Pendelstab von
Hand in die Startposition (senkrecht nach oben und unten gerichtet) gebracht werden, damit diese als Nullpunkt bezüglich des Pendelwinkels definiert werden kann. Während der Regelung kann der
Benutzer den Wagen positionieren. Die Sollwertvorgabe erfolgt dabei entweder über den Joystick oder die Tastatur des Prozeßrechners.
7 Ergebnisse
7.1 Besondere Eigenschaften des Zustandsreglers
Eine andere Vorgehensweise bei der Lastkran- oder Balance-Regelung sieht den Einsatz zweier Reglerkreise vor, von denen einer für die Positionierung des Wagens und einer für die Ausrichtung des Pendelstabes zuständig ist. Diese Methode wird auch beim Einsatz der Fuzzy-Technologie verwendet [4]. Zu den besonderen Eigenschaften des Zustandsreglers gehört die Anschaulichkeit des Regelvorganges. Da die Prozeßdaten mit einem konstanten Faktor multipliziert und anschließend summiert werden, wird sofort der Einfluß von Änderungen der Prozeßdaten auf die Stellgröße deutlich (Abb. 19: Kurvenverläufe der errechneten Prozeßgrößen).
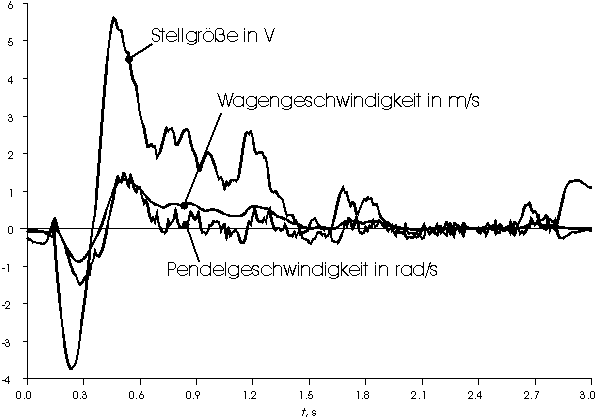
Abb. 19: Kurvenverläufe der errechneten Prozeßgrößen
Dieses führt allerdings auch dazu, daß sich Störungen bei der Meßwerterfassung - zum Teil noch erheblich verstärkt - direkt auf die Stellgröße auswirken. Hinzu kommen die Ungenauigkeiten bei der
Berechnung der Geschwindigkeiten durch numerische Ableitung.
Die "gestörte" Stellgröße führt zu einem ungünstigen Verhalten des Pendelwagens (ruckartige Bewegungen), welches wiederum Meßfehler erzeugt. Abhilfe wurde durch die Konstruktion des stabileren
Pendelwagens und den Einsatz von Filtern in der Regelungssoftware geschaffen.
Eine interessante Erscheinung konnte bei der Balance-Regelung beobachtet werden. Wurde der Pendelstab beim Start nicht exakt senkrecht gehalten, führte dieses zu einer bleibenden Regelabweichung
bezüglich der Wagenposition. Die Erklärung dafür steckt im Prinzip des Zustandsreglers: Wenn der Pendelstab im Moment der Initialisierung nicht exakt senkrecht nach oben gerichtet ist, dann wird
zu dem Zeitpunkt, zu dem durch den Balanciervorgang der Pendelstab senkrecht steht, ein Winkel ungleich Null gemessen. Der Zustandsregler erkennt, daß der Pendelstab senkrecht steht (s. u.) und
erzeugt er eine Stellgröße von annähernd Null. Da sich die Stellgröße aus der Summe der Produkte der Prozeßdaten multipliziert mit den konstanten Reglerkoeffizienten errechnet, muß das durch den
falschen Winkelwert erzeugte Ungleichgewicht ausgeglichen werden. Dieses wird dadurch erreicht, daß der Wagen nicht exakt seine Sollposition einnimmt. Die dabei entstehende Abweichung,
multipliziert mit dem zugehörigen Reglerkoeffizienten, ergibt denselben Betrag wie das Produkt aus Winkelwert und dem entsprechendem Reglerkoeffizienten. Durch die unterschiedlichen Vorzeichen
dieser Werte ist das Gleichgewicht wiederhergestellt und das System befindet sich in einem stationären Zustand.
Bleibt die Frage zu klären, warum der Zustandsregler nicht versucht, die Position des Pendelstabes so zu beeinflussen, daß der Winkel den Wert Null annimmt. Offensichtlich ist dieses nicht das
vorrangige Ziel des Zustandsreglers. Betrachtet man die Reglerkoeffizienten, wird einem die starke Gewichtung der Pendelgeschwindigkeit offenbar. Der Zustandsregler versucht nicht, die
Pendelposition auf den Wert Null zu bringen. Vielmehr liegt die Priorität bei der Geschwindigkeit, mit der sich der Pendelstab bewegt. Ist diese annähernd Null, so steht das Pendel senkrecht. Ob
dieses "senkrecht" einen gemessenen Winkel ungleich Null bedeutet, spielt nur eine untergeordnete Rolle.
| Besonders deutlich wird diese Eigenschaft des Zustandsreglers, wenn der Versuchsaufbau an einer Seite angehoben wird (Abb. 20: Versuchsaufbau geneigt). Der Pendelwagen bewegt sich zur niedrigeren Seite der Gleitschiene hin. Allerdings nicht, um den Gesetzen der Schwerkraft zu folgen, sondern mit dem Ziel, den gemessenen Winkelwert auszugleichen - wie oben beschrieben. |
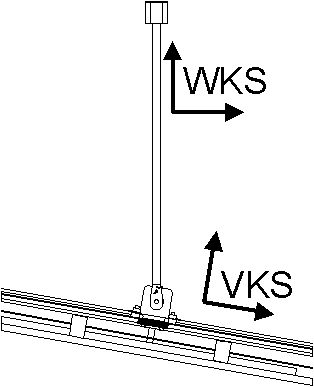 Abb. 20: Versuchsaufbau geneigt |
Währenddessen wird der Pendelstab weiter balanciert. Er bleibt senkrecht, bezogen auf das Weltkoordinatensystem (WKS), während er bezogen auf das Koordinatensystem des Versuchsaufbaues (VKS) eine geneigte Position einnimmt. Solange der Linearitätsbereich (ca. ±1 rad) des Pendelwinkels nicht verlassen wird und dem Pendelwagen innerhalb des gültigen Verfahrbereiches genügend Strecke zum Ausgleichen des Winkelwertes bleibt, kann der Versuchsaufbau beliebig geneigt werden.
7.2 Vergleich von Simulation und Realität
Um die Simulationsergebnisse mit der Realität vergleichen zu können, wurden mit der TUNING-Version der Regelungssoftware die Prozeßgrößen während der Regelung aufgezeichnet. Somit lassen sich
sowohl für die Lastkran- als auch für die Balance-Regelung das Prozeßverhalten bei einem Sollwertsprung darstellen. Zur besseren Übersicht werden nur drei Größen (Sollwert, Wagen- und
Pendelposition) als Kurvenverläufe dargestellt.
Die dazugehörigen Kurvenverläufe der Simulationen wurden mit den schon beschriebenen Blocksystemdateien unter WinFACT erzeugt. Allerdings erfolgten einige Änderungen: Die Sollwertsprünge der
Simulation wurden denen der Realität angepaßt. Außerdem wurden die Prozeßdaten nicht visualisiert, sondern durch die dafür vorgesehenen Ausgangs-Blöcke in Dateien gespeichert. Bei den
Darstellungen der realen Prozeßgrößen zeigen die Kurvenverläufe der Pendelposition deutlich die Störungen, mit denen die Messung dieser Größe behaftet ist. Gerade bei der Balance-Regelung, bei
der dieser Wert großen Einfluß auf die Stellgröße hat, macht sich dieser Umstand auch bei der Wagenposition bemerkbar. Um so erstaunlicher ist die frappierende Ähnlichkeit der jeweiligen
Kurvenverläufe (Simulation/Realität). Vor allem die Lastkran-Regelung zeigt in der Realität (Abb. 21: Kurvenverläufe der realen Lastkran-Regelung) exakt das nach der Simulation (Abb. 22:
Kurvenverläufe der simulierten Lastkran-Regelung) zu erwartende Verhalten.
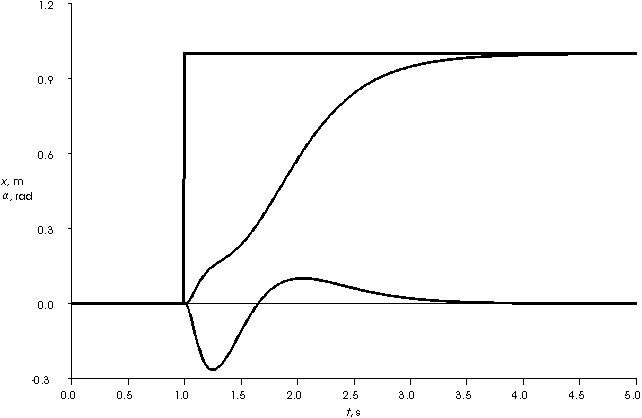
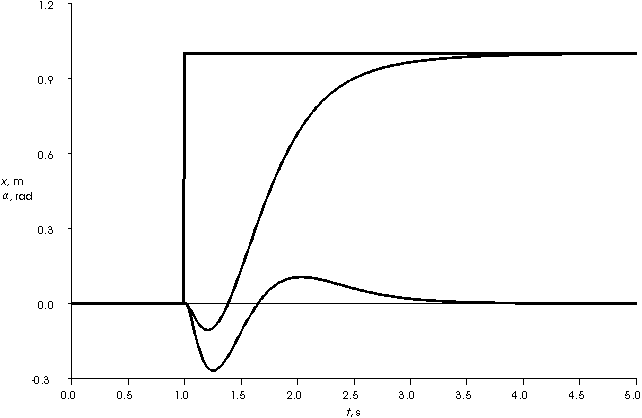
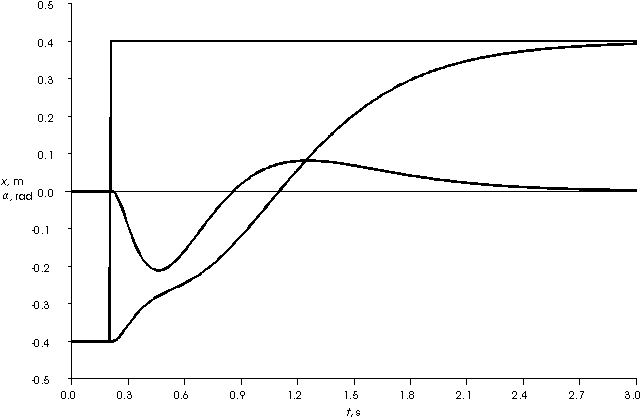
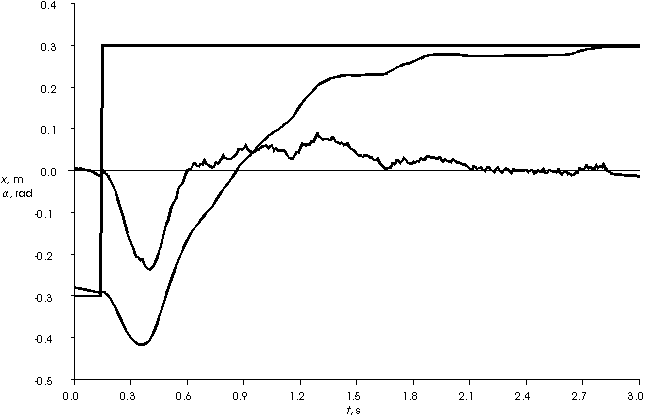
Bei der Balance-Regelung (Abb. 23: Kurvenverläufe der realen Balance-Regelung) sind trotz der Filterung der Meßwerte immer noch starke Störungen zu erkennen. Dadurch entspricht das Verhalten
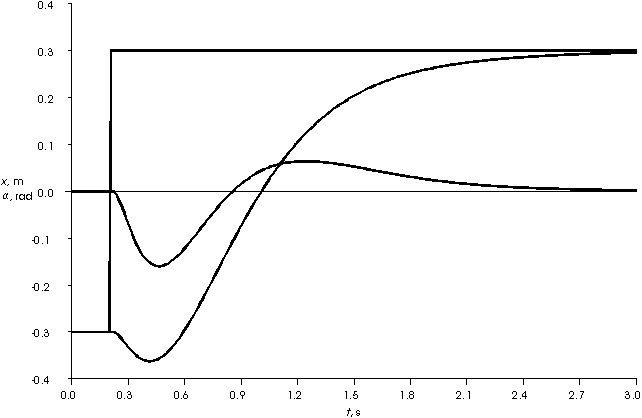
nicht exakt den simulierten Daten (Abb. 24: Kurvenverläufe der simulierten Balance-Regelung).
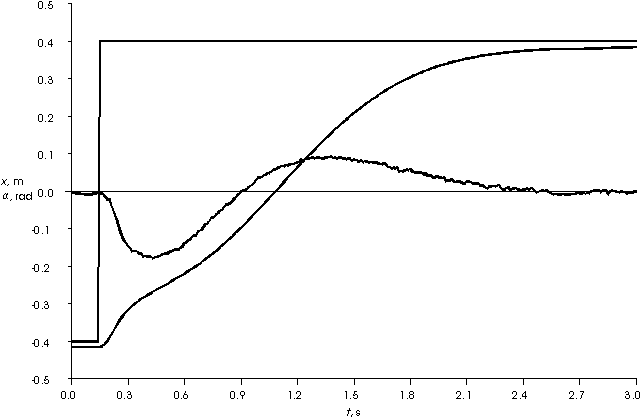
Abb. 21: Kurvenverläufe der realen Lastkran-Regelung
Abb. 22: Kurvenverläufe der simulierten Lastkran-Regelung
Abb. 23: Kurvenverläufe der realen Balance-Regelung
Abb. 24: Kurvenverläufe der simulierten Balance-Regelung
8 Schlußfolgerungen und Ausblick
In der vorliegenden Arbeit wurde durch systematische Analyse ein Regler für die Lastkran- und Balance-Regelung entworfen. Die Ergebnisse zeigen, wie nah Simulation und Realität in diesem Fall
zusammenliegen. Die Probleme auf dem Weg zu diesem Ziel lagen auf Seiten der Meßtechnik, da ohne brauchbare Meßwerte die beste Regelung keine verwertbaren Ergebnisse liefern kann. Diese Tatsache
sollte zu einer Sensibilisierung bezüglich solcher Problematiken führen. Für weiterführende Diplomarbeiten bieten sich folgende Aufgabenstellungen an: Zur Zeit muß für die Balance-Regelung der
Pendelstab von Hand in die senkrecht nach oben gerichtete Position gebracht werden. Dieser Vorgang sollte automatisiert werden. Dazu wird ein Regelalgorithmus benötigt, der den Pendelstab zum
Schwingen bringt, bis dieser annähernd die gewünschte Position erreicht. In diesem Moment muß von dem Aufschwing-Regler zu dem Balance-Regler umgeschaltet werden. Ein Beispiel für eine solche
Aufschwing-Regelung findet sich bei [1].
Desweiteren wäre eine Stabilitätsanalyse interessant. Dabei sollte festgestellt werden, bis zu welchem Grade die Pendelstablänge geändert werden darf. Um dieses zu erreichen empfiehlt es sich,
durch ein zusätzliches Gewicht den Schwerpunkt des Pendelstabes zu verlagern. Dieses Gewicht kann an dem dafür vorgesehenen Aufnahmewinkel befestigt werden. Soll die Manipulation des
Schwerpunktes während der Regelung erfolgen, kann statt des Gewichtes auch ein Gefäß befestigt werden, welches z. B. mit Kugeln gefüllt wird [5]. Im Zusammenhang mit der
Stabilitätsanalyse kommt der Einsatz eines Fuzzy-Reglers in Betracht. Wie schon Untersuchungen an anderer Stelle ergaben [5], sind Fuzzy-Regler nahezu unempfindlich gegenüber
Änderungen der Prozeßparameter. Bei dem Entwurf eines Fuzzy-Reglers gibt es verschiedene Ansätze [4, 5, 8, 9, 10], die alle zu ähnlichen Ergebnissen kommen.
9 Literaturverzeichnis
[1] M. Kluge, M. Thoma: Aufschwingen eines Pendels mit strukturvariablem Regler. at 38 (1990) 3, S. 114-117, R. Oldenbourg Verlag
[2] M. Kluge, M. Thoma: Beobachtergestützte Regelung eines Doppelpendels. at 39 (1991) 9, S. 304-309, R. Oldenbourg Verlag
[3] H. Unbehauen, H. Meier zu Farwig: Optimale Zustandsregelung eines stehenden Dreifachpendels. at 38 (1990) 6, S. 216-222, R. Oldenbourg Verlag
[4] Torsten Bertram, Ferdinand Svaricek: Zur Fuzzy-Regelung eines aufrechtstehenden Pendels. at 40 (1992) 8, S. 308-310, R. Oldenbourg Verlag
[5] Prof. David Dyntar: Fuzzy Logic Control im Vergleich mit modellbasierten Entwurfsverfahren. Zentralschweizerisches Technikum Luzern, März 93
[6] Martin Zirpel: Regelungstechnik mit PC-Simulation: Regelungsvorgänge erfolgreich am PC simulieren und optimieren. Franzis-Verlag, 1994
[7] Robert Kress: Eigene Hardware im PC: Prototyp-Karte für PCs. c't 9/1986, S. 78-79, Heise-Verlag
[8] Hans-Heinrich Bothe: Fuzzy-Logic: Einführung in Theorie und Anwendungen. Springer-Verlag, 1993
[9] Marco Böll, Martin Höttecke, Frank Dörrscheidt: Analyse von Fuzzy-Reglern in der Zustandsebene. at 41 (1993) 5, S. 145-151, R. Oldenbourg Verlag
[10] Günter Ludyk, Gerd-J. Menken: Unscharf oder einfach? - Fuzzy-Regelung im Vergleich. at 42 (1994) 6, S. 264-270, R. Oldenbourg Verlag
Technische Daten Versuchsaufbau |
|
| Pendelstablänge | 0,465 m (Schwerpunktabstand) |
| maximaler Verfahrweg | 0,95 m (Abstand der inneren Endtaster) |
| Auflösung Pendelwinkel | 3E-3 rad |
| Auflösung Wagenposition | 45E-6 m |
| Prozeßrechner | IBM-kompatibler 486DX33; PC-Lab-Karte Typ PCL-812PG; Prototyp-Platine (Eigenentwicklung) |
| Antrieb | DC-Servoverstärker GS 26.40.1, Sieb & Meyer, Lüneburg; Gleichstrom-Servo-Motor Typ P510, GSC, Friedrichshafen |
| Meßtechnik | MOES 500, optoelektronischer Impulsgeber, MEGATRON; Dinopot, Präzisions-Leitplastikpotentiometer, Baureihe P1701 |
| Abtastzeit der Regelungssoftware | 10 ms |
| Verstärkung des Servoverstärkers (K) | 0,265 m/sV |
| Zeitkonstante des Servoverstärkers (T) | 0,12 s |
Bilder vom Versuchsaufbau
Dieses Bild zeigt den Pendelwagen. Im Vordergrund ist der Flansch zu sehen, in dem sich das Potentiometer und die Meßelektronik befinden. Die Konstruktion ist auf Robustheit ausgelegt und sorgt
durch ihr Gewicht für eine Dämpfung des gesamten Systems.
Hier sieht man den Motor und den Pendelwagen beim Balancieren des Pendelstabes.
Aus dieser Perspektive ist vorne die Umlenkrolle mit ihren Spannschrauben zu erkennen. Im Hintergrund befindet sich der Antriebsmotor mit dem Impulsgeber auf dem linken Ende der Antriebsachse.

 Inhalt
Inhalt